AlphaGo背后的卷积神经网络（一）

机器学习

Alpha Go 与李世乭的围棋对弈向大家展示了人工智能的强大，大部分围棋专业人士都在称赞 Alpha Go 有大局观，下棋像人的思维。这次比赛必定将成为人工智能技术的一个里程碑。与20年前IBM的深蓝战胜人类国际象棋大师卡斯帕罗夫相比Alpha Go在技术方面有着明显的不同，深蓝的算法中对棋局的判断是通过一个人工编写的评估函数来执行的，这个评估函数是科学家和人类国际象棋高手共同完成的，可以说深蓝的胜利是众多国际象棋高手和计算机科学家对卡斯帕罗夫的胜利。但是对于围棋而言，人类建立的围棋理论相当抽象，无法写出有效的评估函数，所以Alpha Go采用了深度学习的方式，通过大量数据的有监督学习，从而获得了一个围棋局势评估的模型。通过DeepMind发表在《自然》的论文，我们可以知道Alpha Go 由两套卷积神经网络和一棵蒙特卡洛树组成，其中一套被称作策略网络的卷积神经网络用于决定下一步落子可能的位置，另一套被称作值网络的卷积神经网络用于评估当前棋局获胜的概率。毫无疑问，Alpha Go 的胜利证明了卷积神经网络的强大和通用性。接下来这里讲尽可能通俗地介绍一下卷积神经网络。

卷积神经网络简介

卷积神经网络是一种特殊的深度人工神经网络。卷积网络最初是受视觉神经机制的启发而设计的，是为识别二维形状而设计的一种多层人工神经网络，这种网络结构对物体平移、比例缩放、倾斜或者共他 形式的变形具有高度不变性。1962年 Hubel 和 Wiesel 通过对猫视觉皮层细胞的研究，发现了处理视觉信息的不同神经元只对图片的局部信息敏感，从而提出了感受野(receptive field)的概念，1984年日本学者 Fukushima 基于感受野概念提出的神经认知机(neocognitron)模型，它可以看作是卷积神经网络的第一个实现网络，也是感受野概念在人工神经网络领域的首次应用。我们不用去纠结生物神经学里的各种概念，卷积神经网络只是受到了生物学的启发而已并不是完全模仿生物的视觉神经系统。

我们可以把卷积神经网络分成两个部分：卷积抽样层和BP神经网络。其中卷积抽样层的作用是从原始的数据（例如图像数据）中提取出让BP神经网络能够进行分类的特征数据。例如在图像识别领域为了完成图片的分类需要通过特定的图像处理程序来获取图片的特征例如边缘轮廓特征，色彩分布特征等，但是事实上这些特征不是最适合通过机器学习的模型进行分类的特征，深度学习的思路就是利用机器学习的方式来获取适合机器模型的特征，卷积神经网络里面一般使用BP神经网络作为分类器。

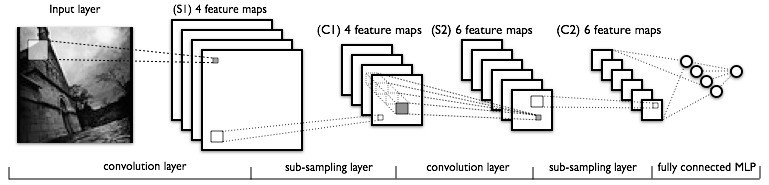
卷积神经网络结构
图1

如上图展示的那样分成两个部分：左边是两个卷积层和采集层，最右边是一个BP神经网络。

卷积运算

卷积运算操作是源于信号处理的一种滤波运算，例如为了降低信号噪音的高斯过滤，我们把图像看出一种信号源，那么卷积操作也就可以被用于图像相关的各种过滤操作，例如前面提到的高斯滤波卷积运算应用于图像就是我们常用的图像处理效果高斯模糊。卷积运算是物理学家发明的运算，但是它有着严谨的数学逻辑，但我们这里不打算展开推导卷积运算的过程，我们可以把卷积运算理解为：“加权平均积”。对于图像处理我们都是采用的二维卷积，本文以下部分的卷积都是指的二维卷积。对于图像处理的卷积运算可以表达为如下的公式：

$$g(i,j) = \sum_{k,l}f(i-k,j-l)h(k,l)$$

上面公式中h被称作卷积核或者卷积算子，f就是需要处理的位图，f(i,j)表示位图上坐标为(i,j)点上的颜色值。公式看起来还是比较抽象，下面这张图就更好的解释了卷积计算是如何进行的。

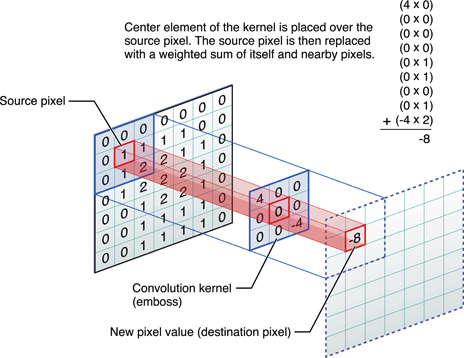
卷积神经网络结构
图2

上图中一个3*3的卷积核在图片上分别按横轴和纵轴逐像素移动，卷积核的中心点对应的图片像素点的颜色值被赋值为卷积核上与图片对应像素点的颜色的乘积和。

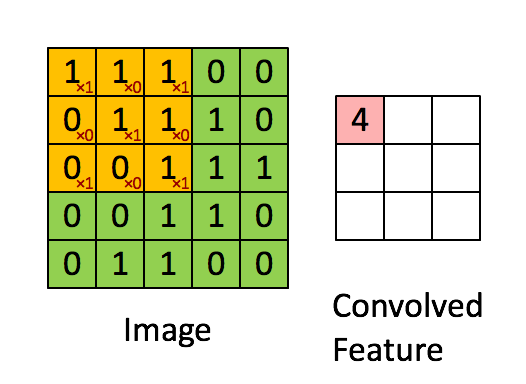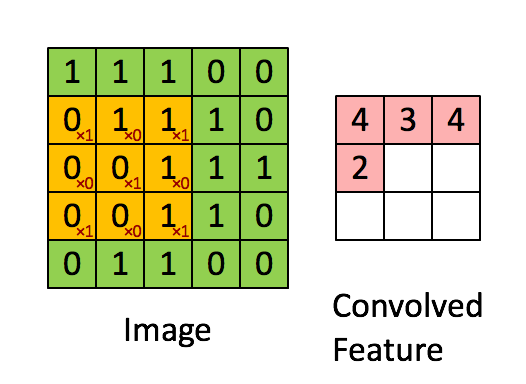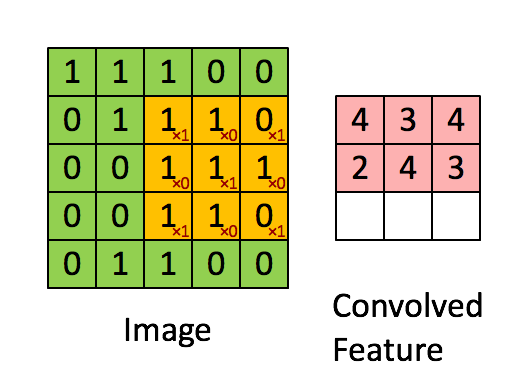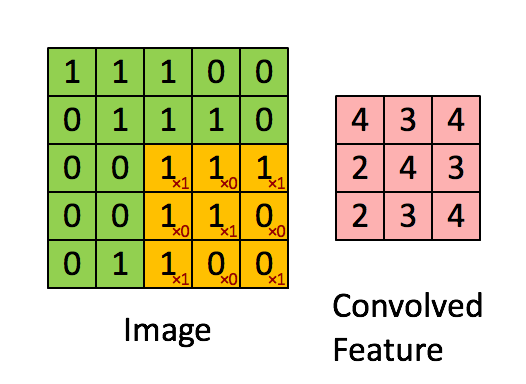
卷积神经网络结构
图3

例如上图已经演示了利用如下卷积核对位图进行卷积的操作
$$
\left[
\begin{array}{cc}
1 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 1
\end{array}
\right]
$$

卷积后位图(2,2)位置的颜色值被赋值为4,具体计算过程为:

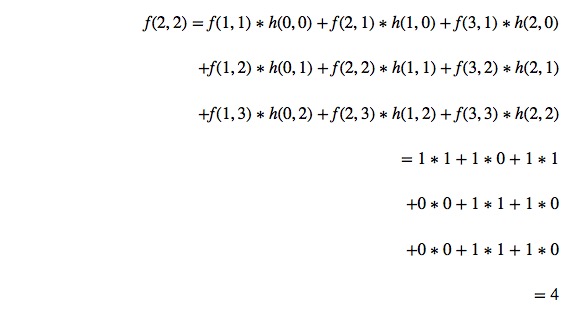
对于卷积运算后像素颜色值超过255的问题可以使用均值为0的归一化算法处理。

卷积运算的作用

卷积运算本身并不复杂，但是它实际的意义是什么呢？

抛开信号处理相关的数学理论，从一个便于理解的角度来讲二维卷积就是通过卷积运算让图像中某一点接收周围像素的影响把自身的颜色值变大或者缩小，具体缩小还是放大取决于卷积核的取值。例如我们sobel卷积核对图片进行卷积运算，可以让图片中的所有边缘轮廓变亮而非边缘轮廓的部分都变暗。
卷积前的图片

卷积神经网络结构
图4

卷积后的图片

卷积神经网络结构
图5

对于整个卷积神经网络而言语卷积核就是一个矩阵，通过卷积运算可以获取更便于识别的特征。卷积核是通过监督学习获取的，我们先随机初始化一个卷积核，通过BP神经网络反馈过来的损失值会被用于调整卷积核的值。

局部采样

卷积神经网络的前半部分除了卷积运算外为了减少复杂度还需要进行局部采样。一般情况下都是采样最大值采样，如下图所示最大值采样就是从图片的一个区域中找到颜色值最大的那个点代表整个区域的颜色值。

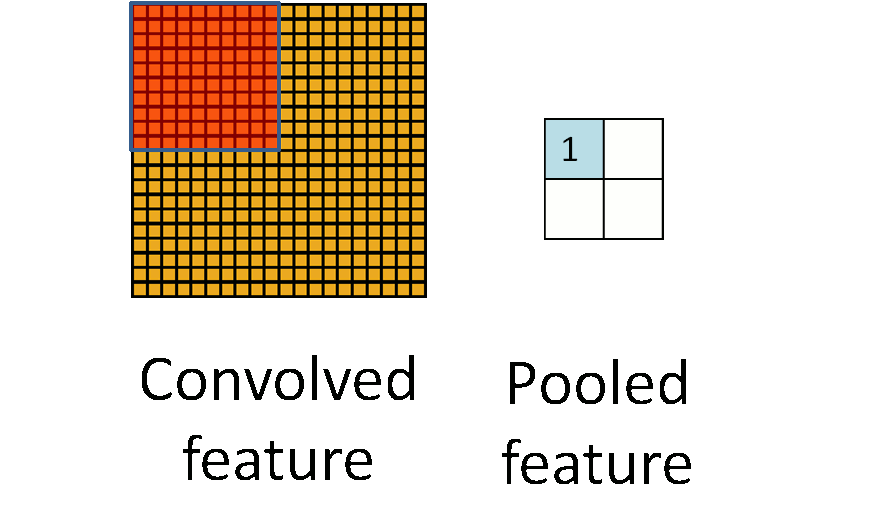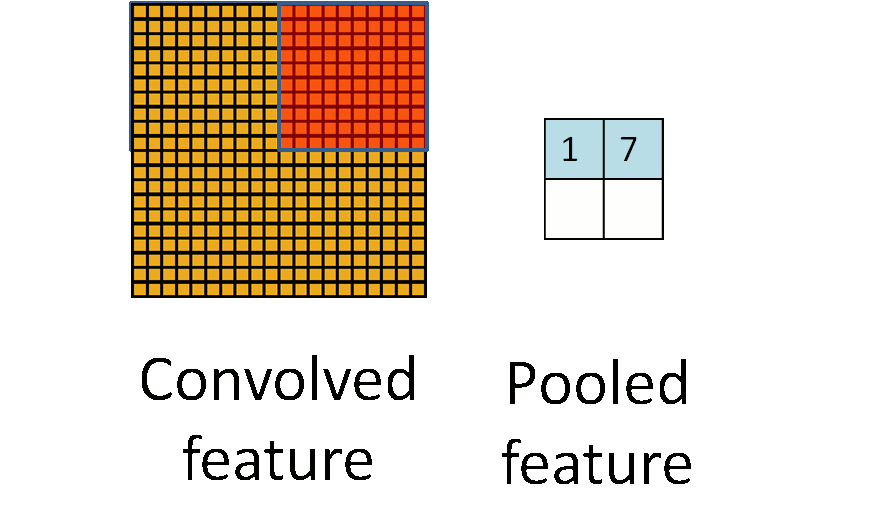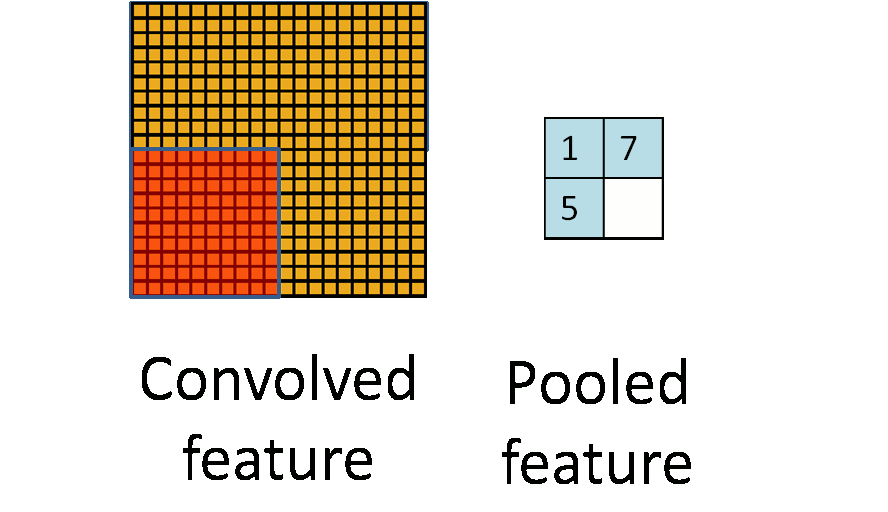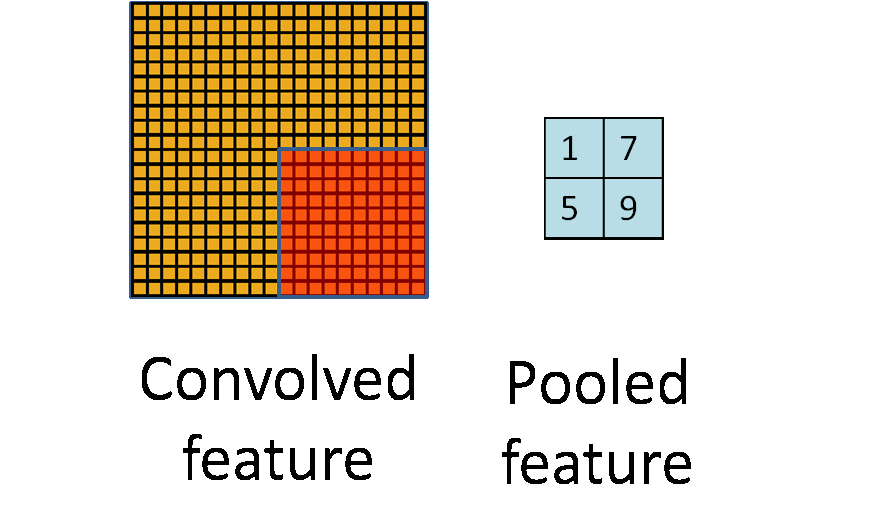
卷积神经网络结构
图6

假设下面矩阵m是位图，我们用一个2*2的最大值采样对m进行采样就会得到矩阵n

矩阵m
$$
\left[
\begin{matrix}
12 & 13 & 6 & 27 \\
31 & 23 & 71 & 45 \\
41 & 93 & 22 & 29 \\
91 & 43 & 23 & 72 \\
\end{matrix}
\right]
$$

采样后得到的矩阵n

$$
\left[
\begin{matrix}
31 & 71 \\
93 & 72 \\
\end{matrix}
\right]
$$

另一种采样方式就是平均值采样。把采样区块内的像素颜色平均值作为采样后的结果，对矩阵m进行2*2的平均值采样将得到下面的矩阵。

$$
\left[
\begin{matrix}
19.75 & 37.25 \\
67.0 & 36.5 \\
\end{matrix}
\right]
$$

我们现在已经清楚了卷积神经网络特征提取部分的基本原理，下一步我们将继续探索卷积神经网络的网络结构和训练相关的内容

本文图片均来自互联网，出处如下：