上篇文章我们介绍了用数学模拟单个神经元而建立的神经元数学模型，这个数学模型可以让我们通过数学运行来实现对数据进行识别，已经某种程度上模拟了生物神经元的工作方式，但是这种模拟并没有太激动人的地方，因为智能的神奇之处在于能够通过学习获取对事物的认知能力。人类具有的生物智能学习能力让人类创建了人类文明，并且能够让人类文明永远的传承下去。所以学习能力对于智能的构成何等重要无需累述。但是鉴于生物大脑结构的复杂性和伦理限制，完全揭示生物学习能力的奥秘还需要科学家的加倍努力。

现在神经科学已经了解了生物大脑学习能力的很多特征，通过一些有趣的实验可以证明通过同样的学习机制生物大脑可以识别不同的信号例如视觉听觉。下面是 Andrew Ng 在斯坦福机器学习公开课上引用的三个例子：

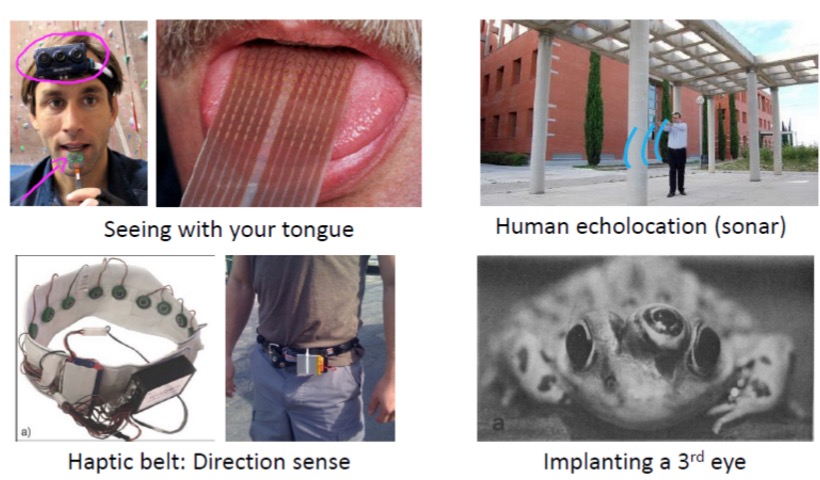
第1行图片，把三个超声波测距仪通过导线接触人的舌头上，通过训练人可以根据舌头的感觉绕开障碍物。第2行图片第1张图片是把方向传感器通过腰带传递信号给人的腰部，人通过训练依据触觉可以判别方向。最后一张图片，人们给一只青蛙移植了第三只眼睛，通过一段时间的适应，青蛙可以对第三只眼睛看到的移动物体做出正确的反应，说明青蛙的大脑已经学会了处理三只眼睛同时提供的视觉信号。

这些实验证明了人脑中的神经元具有一定的通用性，也就是某种用途的神经元通过训练也能够识别其他用途的信号。所以我们通过数学模拟的神经元也应该具有通用性，其实通过数学可以证明，只要足够多的人工神经元几乎可以拟合出任何非线性输出结果。

神经元是通用的，那么接下来我们就需要思考学习过程能不能通过数学来进行模拟。前面文章介绍的通过信息熵的方式来构建决策树和随机森林已经证明了通过数学我们可以模拟生物的学习过程，但是神经元的学习过程又怎么模拟呢？

上篇文章给出的人工神经元模型，我们已经明确了为了让人工神经元能够工作起来，我们需要给出树突和轴突对应的权重值，那么问题就转化成了通过学习的方式从已经有的数据中计算出权重值。最直接的思路就是把权重值当成未知数，列出方程，然后求解就行了。但是，识别的结果往往只是数据的类别，只能列出不等式方程，并且这些方程并不是唯一解，而我们需要的是唯一解，最好还是最优解。BP神经网络就是一种可以自动从已有数据中解算各种权重的人工神经网络。

接下来，我们来看BP神经网络的结构，下图是BP神经网络的示意图。

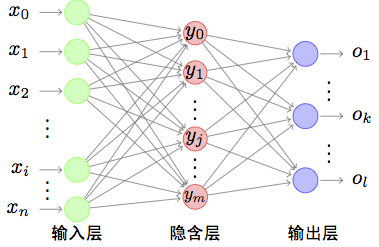
BP（Back Propagation）神经网络是一种多层前馈神经网络。为了方面介绍我们只讨论三层的情况。如上图所示，三层分分别为输入层、隐藏层、输出层。

• 输入层: 接收输入数据不做运算和处理，只会把数据和信号传递给隐藏层，输入层的每个节点都会将信号传递给隐藏层的每个神经元，输入层的节点数量与输入的信号维度相同；
• 隐藏层: 包含多个人工神经元，每个神经元接收多个输入节点的信号并把这些信号的值与接收树突的权重相乘并累加起来，最后调用sigmoid函数输出给输出层。
• 输出层：隐藏层的每个神经元把sigmoid的结果传递给每个输出层的神经元，输出层和隐藏层一样会进行权重相乘并累加的处理，最后调用sigmoid函数作为整个神经网络的输出。

BP神经网络训练算法的基本思路就是不断循环调整各个神经元树突的权重值，使得BP神经网络的输出与训练样本期望值的误差最小。 按照这个思路我们需要用一个函数来衡量误差，还需要找到一个数学方法来调整各个权重值。

有多种函数可以衡量BP神经网络的输出误差，衡量输出误差的函数被称为代价函数（Cost Function）,最常见的代价函数为二次代价函数和交叉熵代价函数。

二次代价函数:

$$E=\frac{1}{2}(y-O)^{2}$$

训练时我们通常是需要衡量一批数据的误差，批量数据的二次代价函数为：

$$E=\frac{1}{2}\sum_{k}^{l}(y-O)^{2}$$

公式中的O表示就是各层的输出，y表示训练数据的标注的分类。现在的求解树突权重的问题可以转变为求解当二次代价函数取最小值时各个树突权重的值。我们可以采用梯度下降算法来求解各个树突的权重。梯度下降算法的思路就是按一定的步长不断调整权重值让代价函数的值变小。

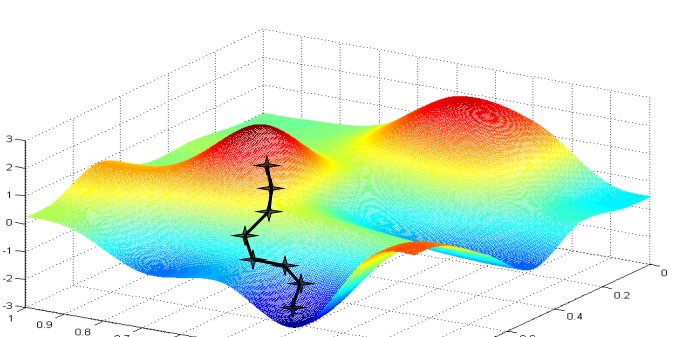
如上图，可以把代价函数看成一个曲面（大部分情况树突的权重值的数量不止3个，所以代价函数应该是一个超平面），为了找到最小值我们可以按照代价函数梯度下降最快的方向不断尝试调整树突的权重，最终找到整个曲面的最低点，也就是梯度不再下降的点。

下面我们将直接给出权重调整的公式。

激励函数sigmoid关于x导数为：
$${f}’(W)=\frac{\partial f}{\partial W_{ij}}=O_{ij}(1-O_{ij})$$

输出层权重调整公式：

$$\delta _{o}=\frac{\partial E}{\partial W_{i}}=O_{j}(1-O_j)(y_{j}-O_{j})$$

隐患层权重调整公式：

$$\delta _{h}={f}’(W)(\sum W_{ij}\delta _{o})$$

上面公式中i表示权重的下标，j表示神经网络的层次。每一个训练批次，调整权重的公式为：

$$W_{ij} = W_{ij}-\eta \delta W_{ij}$$

上面公式中$\eta$ 表示学习率也就是我们每次尝试调整权重的步长，如果步长太大，容易错过代价函数的最小值从而得不到权重的最优解，一般情况下我们会把 $\eta$ 设置为0-1之间的一个值。从上面的公式可以看出调整权重的过程就是分别计算出$\delta _{o}$和$\delta _{h}$,然后权重减去用$\delta _{o}$和$\delta _{h}$乘以对应层的权重。清楚了计算公式以后，接着我们来看训练过程。

BP神经网络的训练过程分成两个阶段：

• 向前传递：对于一批数据从输入层接收数据然后传递给隐藏层，隐藏层又传递给输出层，最后得到输出层激励函数的输出；
• 向后传递：根据网络的输出和训练数据的标注计算出权重的调整值，然后对各层的权重就行调整；

其实，数学理论可能会让你头晕，但是看看具体的代码看起来就清晰多了，,只采用了不到60行代码就是实现了一个简单明了的BP神经网络。

# coding: utf-8

import numpy as np

# 隐藏层神经元数量
hiddenSize = 32


# 激励函数
def sigmoid(x):
    output = 1 / (1 + np.exp(-x))
    return output


# 激励函数的导数
def sigmoid_derivative(output):
    return output * (1 - output)


def train(X, y):

    np.random.seed(1)
    # 学习率
    eta = 0.01
    # 随机初始化隐藏层和输出层的权重，让权重的平均值为0
    synapse_hidden = 2 * np.random.random((3, hiddenSize)) - 1
    synapse_output = 2 * np.random.random((hiddenSize, 1)) - 1

    for j in xrange(60000):

        # 向前传播计算出各层输出
        layer_input = X
        layer_hidden = sigmoid(np.dot(layer_input, synapse_hidden))
        layer_output = sigmoid(np.dot(layer_hidden, synapse_output))

        if (j % 10000) == 0:
            layer_output_error = layer_output - y
            print "Error after " + str(j) + " iterations:" + str(np.mean(np.abs(layer_output_error)))

        # 计算输出层调整值
        layer_output_delta = (layer_output - y) * sigmoid_derivative(layer_output)
        # 计算隐藏层调整值
        layer_hidden_delta = layer_output_delta.dot(synapse_output.T) * sigmoid_derivative(layer_hidden)
        # 调整权重
        synapse_output -= eta * (layer_hidden.T.dot(layer_output_delta))
        synapse_hidden -= eta * (layer_input.T.dot(layer_hidden_delta))

X = np.array([[0, 0, 1],
              [0, 1, 1],
              [1, 0, 1],
              [1, 1, 1]])

y = np.array([[0],
              [1],
              [1],
              [0]])

train(X, y)

上面的代码已经非常清晰了。

上面的代码已经是一个可以运行的BP神经网络了，但是这段代码并不能真正地应用于实际工程应用，由于这段代码忽略了偏置值，另外由于BP神经网络涉及到的权重比较多容易过拟合，为了解决容易过拟合问题需要采用Dropout技术，每一批次数据都随机放弃更新部分权重。

接下总结一下BP神经网络的优缺点和应用情况。

BP神经网络有以下的一些优点：

• 泛化能力，BP神经网络的泛化能力是指当向网络输入一些训练时未曾遇到的样本时，它可以正确地将未知样本进行分类和预测等，也就是完成由输入空间到输出空间的正确映射，泛化能力也是衡量一个模型性能优劣的重要因素，BP神经网络通过实践证明有较好的泛化能力。
• 容错能力，BP神经网络的容错能力是指允许输入样本带有个别误差，因为神经网络的训练过程也是一个提取统计特征的过程，个别的误差不会影响到整个网络的训练。

BP神经网络在实际的应用中也存在着以下的缺点：

• 容易陷入局部极小而得不到全局最优。在实际的计算中，我们希望BP网络可以找到全局最优点，但往往它会陷入局部最优点，这也表明问题的主要特征没有被网络所提取出来。在这种情况下，通常通过初始化权值再重新训练一遍的方面可以避免，也可以采用Dropout方法放弃更新一些权重。
• 收敛速度慢。由于BP神经网络的优化方法是梯度下降法，它所要优化的目标函数是一个复杂的非线性函数，因此训练次数多，而且由于误差曲面上有平坦区域，在这些区域中，误差的梯度变化不大，这也使得收敛速度变慢。
• 缺乏理论指导。目前BP神经网络的建模一般都是根据以有的经验设置网络参数，比如隐层的层数，隐层的节点个数等，这些参数只能根据人工经验调整。

BP神经网络由于被应用于卷积神经网络，递归神经网络的最后部分，所以BP神经网络的应用现在越来越广泛，人脸识别，语音识别，人工智能问答等领域都离不开BP神经网络的应用。有关其应用的最新新闻是Facebook研究围棋算法的负责人透露使用过深度卷积神经网络的训练的模型已经可以战胜围棋业务6段选手。