
这是一篇写机器算法的东西,希望能借此掀开机器学习算法面纱的一角,让我们可以和机器学习算法开始愉快的玩耍。文章开始前,来首泰戈尔的诗烘托一下气氛
The machine learning puts off it’s mask of vastness to it’s love.
It becomes small as one song, as one kiss of the eternal.
(机器学习在情人面前宽衣解带,绵长如舌吻,纤细如诗行–冯唐译本人改编)
机器学习算法是一种自动地从数据中学习的一些算法。与手工编程相比,机器学习非常的有Bigger,充满了黑科技味道,事实上,当数据非常巨大的时候人力很难去正确的了解和掌握数据的全貌和细节,手工编程几乎没有可能,所以机器学习几乎是一种不可缺少的算法了。在过去的20年中,机器学习已经迅速地在计算机科学等领域普及。机器学习被用于网络搜索、垃圾邮件过滤、人脸识别、语音识别、人机对话、推荐系统、广告投放、信用评价、欺诈检测、股票交易,疾病诊断等方面。由于充满了“黑科技“味道,吓退了一大批”战士“,但是我们是那名叫大卫的”牧童“专用黑科技(这句看不懂?参考前面的文章),所以机器学习是我们和大数据周旋的大杀器。机器学习算法中分类算法是一系列非常常用的算法,而随机森林是一种容易理解应用广泛的分类算法,大量的理论和实证研究都证明了随机森林具有很高的预测准确率,对异常值和噪声具有很好的容忍度,且不容易出现过拟合。可以说,随机森林是一种人类好理解的非线性建模工具,是当前数据挖掘算法最热门的前沿研究领域之一。
要了解随机森林,我们必须先了解组成森林的一棵棵决策树。随机森林由多棵决策树组成,同时决策树也可以单独作为分类算法使用。为了那片随机森林我们就先从决策树的训练过程开始吧。决策树是一种监督学习算法,通过训练数据构建决策树的过程就是其算法的核心。
决策树的训练过程就是从一组无次序、无规则的数据中推理出以树形结构表示的分类规则。通常每条数据都有多个属性,而数据的某些属性或者全部属性决定了数据的分类。训练好的决策树的每个叶子节点都表示分类的结果,而非叶节点都根据某一属性进行判断的决策节点。判断一条数据的类别就是从根节点开始“走”到叶节点的过程。如何从数据中自动推理和构建决策树,有多种算法,其中ID3算法是一种基于信息论的算法,实践证明这种算法够简单够有效,便于人类理解。
首先,我们需要了解一下信息论的一个概念:信息熵。信息熵是衡量信息不确定性的度量,按照信息论的理论,当我们被告知一个极不可能发生的事情发生了,例如奥巴马亲吻了金正恩,那我们就接收到了更多的信息,我们看这条消息,多半会说信息量好大;而当我们得知一个非常常见的事情发生了,例如太阳会从东边升起,那么我们就接收到了相对较少的信息量,这个事情我们早知道一定会发生,信息量为0。如何计算信息熵,这里先按下不表,我们先来看看我们的训练样本数据集,假设我们有一个手机APP的用户列表。
| 用户来源 | 性别 | 自定义头像 | 关注微博 | 是否活跃 |
|---|---|---|---|---|
| 微博 | 女 | Yes | FALSE | No |
| 微博 | 女 | Yes | TRUE | No |
| 注册 | 女 | Yes | FALSE | Yes |
| 微信 | 男 | Yes | FALSE | Yes |
| 微信 | 未知 | No | FALSE | Yes |
| 微信 | 未知 | No | TRUE | No |
| 注册 | 未知 | No | TRUE | Yes |
| 微博 | 男 | Yes | FALSE | No |
| 微博 | 未知 | No | FALSE | Yes |
| 微信 | 男 | No | FALSE | Yes |
| 微博 | 男 | No | TRUE | Yes |
| 注册 | 男 | Yes | TRUE | Yes |
| 注册 | 女 | No | FALSE | Yes |
| 微信 | 男 | Yes | TRUE | No |
我们会用上面表格中的数据集计算出一棵决策树,这棵决策树可以根据用户来源、性别、自定义头像、关注微博这四个字段来预测用户的活跃度。根据信息理论,信息熵越大对应事件的不确定性就越大,那么应用决策树进行预测的过程就是信息熵逐步减少的过程,每经过一个节点信息熵就会减少一些,当到达叶节点的时候事件已经确定了,信息熵应该减少到0。构建这棵的过程就是不断找寻能够让信息熵最快下降的路径。
了解了构建决策树的原理和方向,是时候来看看信息熵的计算公式了
公式中P是相关事件的发生概率,公式就是相关事件概率乘以该概率以2为底的对数再加上负号。如果信息涉及到多个事件,那么就把所有事件的信息熵累加起来,所以更通用的信息熵公式为:
通过训练数据集我们可以算出活跃用户的概率为:9/14,非活跃用户的概率为:5/14,代入信息熵公式:
Entropy = -9.0/14.0 * log2(9.0/14.0) - 5.0/14.0 * log2(5.0/14.0) = 0.940
我们计算出给出任何用户信息其信息熵为0.940,然后我们知道任何一个具体的属性信息,都可以降低信息熵,让是否是活跃用户的判断更明确。所以接下来需要计算每个属性的信息熵。
账号来源
| 取值 | 活跃概率 | 不活跃概率 | 取值概率 | 信息熵 |
|---|---|---|---|---|
| 微博 | 0.4 | 0.6 | 5/14 | 0.971 |
| 注册 | 1 | 0 | 4/14 | 0 |
| 微信 | 0.6 | 0.4 | 5/14 | 0.971 |
账号来源信息熵:
1 | 5/14 * 0.971 + 4/14 * 0 + 5/14 * 0.971 = 0.693 |
根据同样的原理,我们可以算出其他属性的信息熵,各个属性信息熵总结如下表:
| 属性 | 信息熵 |
|---|---|
| 账号来源 | 0.693 |
| 性别 | 0.911 |
| 自定义头像 | 0.789 |
| 关注微博 | 0.892 |
属性的熵表示了一旦知道某属性后的信息熵,那么也就是我们知道某条数据的“账号来源”属性,那么信息熵可以降低到0.693,而知道其他属性降低的信息熵都少于“账号来源”属性。构建决策树的时候需要选择信息熵下降最快的路径,这里显然我们应该选择“用户来源”作为决策树的根节点。选择好了根节点后的决策树如下:
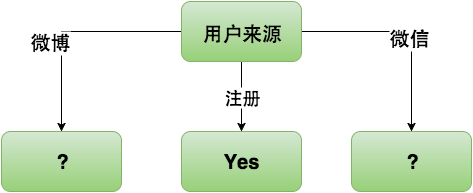
“用户来源”作为根节点,“用户来源”的每个取值都对应一个分支,当“用户来源”取值为“注册”时信息熵为0,所以“注册”分支指向叶子节点为“Yes”。接着我们需要确定“微博”分支和“微信”分支指向的决策节点分别是什么属性。我们可以把“微博”分支和“微信”分支分别看成整棵决策树的“微博”子树和“微信”子树。确定“微博”分支和“微信”分支指向哪个决策节点的过程就是利用训练数据集的子集分别找出“微博”子树和“微信”子树根节点的过程。
下面我们同样通过信息熵的计算来确定“微博”子树的根节点。首先我们把所有“用户来源”属性取值为“微博”的训练数据过滤出来做为训练数据集。
| 用户来源 | 性别 | 自定义头像 | 关注微博 | 是否活跃 |
|---|---|---|---|---|
| 微博 | 女 | Yes | FALSE | No |
| 微博 | 女 | Yes | TRUE | No |
| 微博 | 男 | Yes | FALSE | No |
| 微博 | 未知 | No | FALSE | Yes |
| 微博 | 男 | No | TRUE | Yes |
通过子数据集我们可以知道用户来源为微博的用户中活跃用户的概率为:0.4,而不活跃用户的概率为:0.6,前文我们已经计算出来当用户来源为“微博”的信息熵为:0.971。接下来计算在子数据集中各个属性的信息熵。
自定义头像
| 取值 | 活跃概率 | 不活跃概率 | 取值概率 | 信息熵 |
|---|---|---|---|---|
| Yes | 0 | 1 | 0.6 | 0 |
| No | 1 | 0 | 0.4 | 0 |
通过上表,我们可以看出“自定义头像”的信息熵为:0
性别
| 取值 | 活跃概率 | 不活跃概率 | 取值概率 | 信息熵 |
|---|---|---|---|---|
| 女 | 0 | 1 | 0.4 | 0 |
| 男 | 0.5 | 0.5 | 0.4 | 1.0 |
| 未知 | 1 | 0 | 0.2 | 0 |
性别属性的信息熵为:1.0
关注微博
| 取值 | 活跃概率 | 不活跃概率 | 取值概率 | 信息熵 |
|---|---|---|---|---|
| TRUE | 0.5 | 0.5 | 0.4 | 1.0 |
| FALSE | 1.0/3.0 | 2.0/3.0 | 0.6 | 0.918 |
关注微博的信息熵为:
1 | 0.4 * 1.0 + 0.6 * 0.918 = 0.9508 |
明显选择“自定义头像”属性,信息熵的下降速度最快,所以“微博”子树的根节点为“自定义头像”。由于“自定义头像”的信息熵为0,所以“自定义头像”节点的下层节点是叶子节点。现在我们构建的决策树,“微博”子树已经完成如下图:
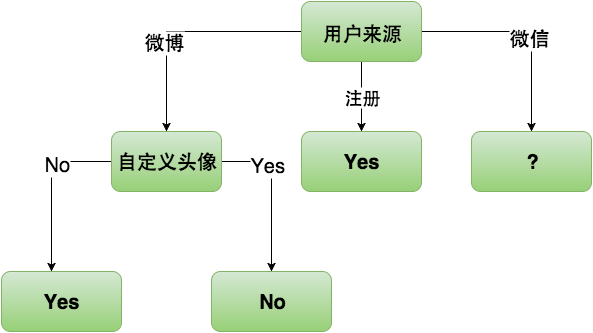
接下来我们来选择“微信”子树的根节点,下面是“微信”子树的训练数据集
| 用户来源 | 性别 | 自定义头像 | 关注微博 | 是否活跃 |
|---|---|---|---|---|
| 微信 | 男 | Yes | FALSE | Yes |
| 微信 | 未知 | No | FALSE | Yes |
| 微信 | 未知 | No | TRUE | No |
| 微信 | 男 | No | FALSE | Yes |
| 微信 | 男 | Yes | TRUE | No |
通过子数据集我们可以知道用户来源为微博的用户中活跃用户的概率为:0.6,而不活跃用户的概率为:0.4,前文我们已经计算出来当用户来源为“微信”的信息熵为:0.971。接下来计算在子数据集中各个属性的信息熵。
性别
| 取值 | 活跃概率 | 不活跃概率 | 取值概率 | 信息熵 |
|---|---|---|---|---|
| 男 | 0.2/0.3 | 0.1/0.3 | 0.6 | 0.918 |
| 未知 | 0.5 | 0.5 | 0.4 | 1.0 |
性别属性的信息熵为:0.9508
自定义头像
| 取值 | 活跃概率 | 不活跃概率 | 取值概率 | 信息熵 |
|---|---|---|---|---|
| Yes | 0.5 | 0.5 | 0.4 | 1.0 |
| No | 2.0/3.0 | 1.0/3.0 | 0.6 | 0.918 |
通过上表,我们可以看出“自定义头像”的信息熵为:0.918
关注微博
| 取值 | 活跃概率 | 不活跃概率 | 取值概率 | 信息熵 |
|---|---|---|---|---|
| TRUE | 0 | 1 | 0.4 | 0 |
| FALSE | 1 | 0 | 0.6 | 0 |
关注微博的信息熵为:0
依据上面的计算,显然“关注微博”属性的信息熵下降得最多,所以“微信”子树的根节点选择为“关注微博”。“关注微博”的取值的信息熵都为0,所以“关注微博”的下层节点都是叶子节点。到此完整的决策树已经构建出来了。
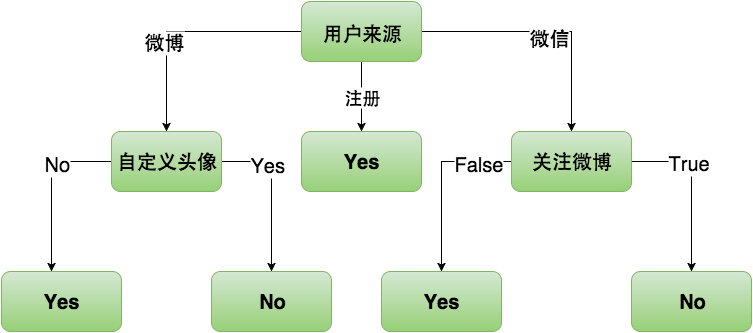
完整的决策树中“性别”属性不见了踪影,由于“性别”信息与是否是活跃用户之间的不确定性太高也就是信息熵过大,所以没有出现在决策树中,这是决策树算法的一个优点,可以排除无用的数据维度。回顾构建决策树的过程,我们不难发现这是一个递归的过程,如果我们用程序来实现ID3算法构建决策树应该是比较简单。当然,决策树也有很多局限性,容易过拟合,不容易处理连续数据,需要训练数据各类别数据量差不多一致,无法处理数据缺失。
为了克服决策树的各种缺点,我们可以构建一片决策树组成的森林,这就是随机森林的出发点。我们下一步征程将是那片森林。